Her er r lufttettheten v er lufthastigheten p er det statiske lufttrykk
½ × r × v2 = "dynamisk trykk" p = "statisk trykk"
BERNOULLIS TEOREM (Kermode s. 59 og 66)
Teoremet forutsetter laminær strømning (ikke turbulent) og
ikke-sammentrykkbar gass eller væske.
Teoremet kan utledes fra at total energi = konstant for et isolert system. For
en "luftpartikkel" i en luftstrøm vil dette si at
Potensiell energi + bevegelsesenergi + trykkenergi = konstant
Ser vi kun på horisontal strømning, kan vi se bort fra potensiell energi, for den endrer seg ikke under strømningen:
Bevegelsesenergi + Trykkenergi = konstant
½ × mv2 + F× s = konstant
½ × r V× v2 + pA× s = konstant
½ × r V× v2 + p× V = konstant
![]()
Her er r lufttettheten v er
lufthastigheten p er det statiske lufttrykk
½ × r ×
v2 = "dynamisk
trykk" p = "statisk trykk"
Dette er kjent som Bernoullis teorem eller Bernoullis ligning.
Eksempler


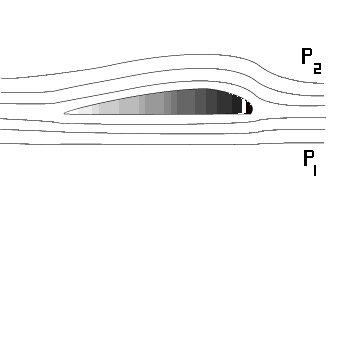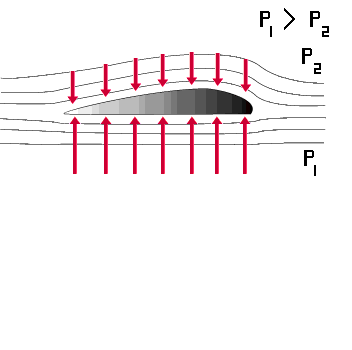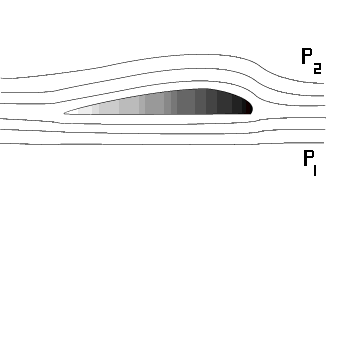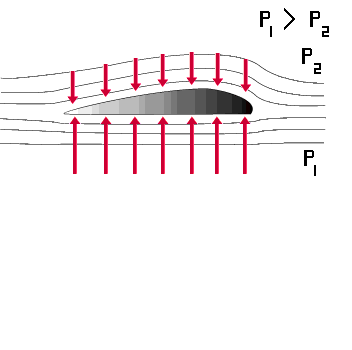


Løftet L
Vi er interessert i å kunne beregne løftet L (benevning [Newton] )
Hvis vi kjenner midlere trykkdifferanse mellom over- og underside av vingen, må løftet bli:
L = p× S der p er midlere trykkdifferanse og S er vingens areal. (Løftet er nesten vinkelrett på vingen og en regner som regel S som vingens kordeareal, selv om det er en liten tilnærmelse).
Trykkdifferansen p kan uttrykkes med Bernoullis teorem som:
p = ½ × r × v2 × CL
Her har vi hoppet over noe mellomregning og innført "konstanten CL som er avhengig av forholdet mellom lufthastighetene over og under vingen, dvs. avhengig av vingens form og angrepsvinkel.
Formelen for løftet blir altså
![]()
Konstanten CL må altså være kjent for det aktuelle vingeprofil og for den aktuelle angrepsvinkel.
Draget D
Merk at draget D som er definert i figuren på forrige side, bare er en
komponent av resulterende kraft pga trykkfordelingen rundt vingen. Vi får
derfor helt tilsvarende beregningsformel for drag som for løft, men
proporsjonalitetskonstanten blir en annen:
![]()
S er fortsatt vingens kordeareal, og den nye "konstanten" CD
(Drag Coefficient) er igjen avhengig av vingeprofilet og angrepsvinkelen.
Eksempel på hvordan CL og CD varierer med angrepsvinkelen for et gitt vingeprofil
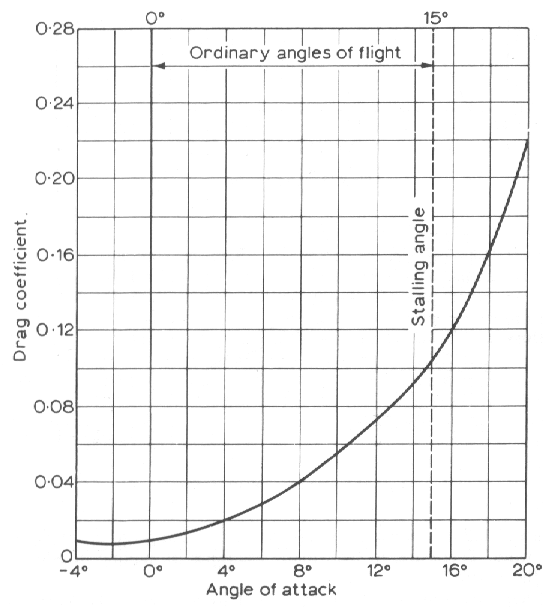
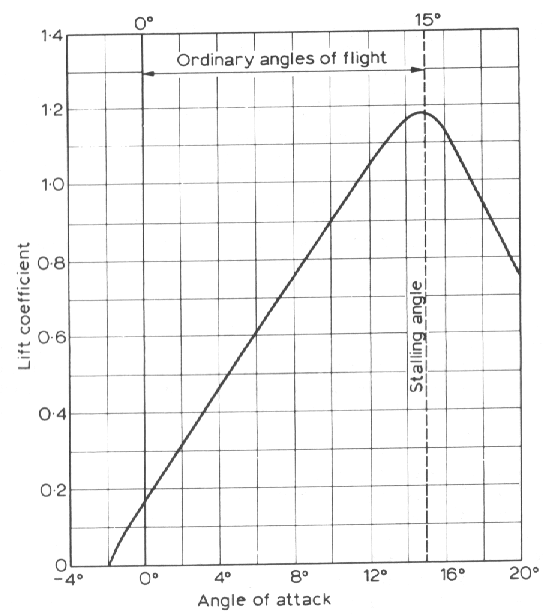
Oppgave.
Et fly bruker vingeprofilet ovenfor, har vingeareal S=20 m2 og
flyr horisontalt med angrepsvinkel a = 8°
og hastighet v = 194 knop (100 m/s) i en høyde der lufttettheten er
r = 1.0 kg/m3.
a) Beregn løft og drag fra vingen
b) Hvilken effekt utvikler motoren?
c) Hvilken masse har flyet?
Oppgave
Ved flyging i 6000 m høyde viser fartmåleren 204 knop (indicated airspeed)
Fartsmåleren bruker et pitotrør (Kermode s.59-63)
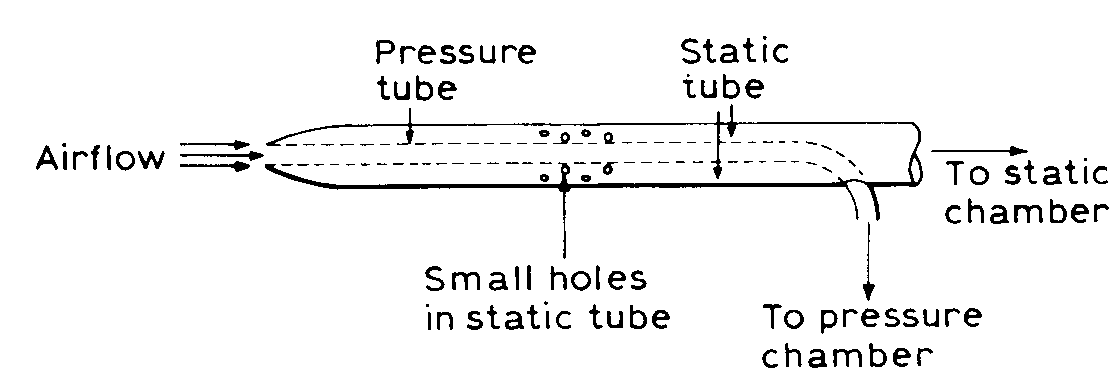
a) Bruk Bernoullis teorem og finn trykkdifferansen (p’-p) i pitotrøret.
b) Hva er flyets "True Airspeed" hvis vi antar normalatmosfære (figur i Kermode s. 35)?
Les om "VINDTUNNELL"
Kermode s. 43-49 (9. utgave)
Lufthastighet, trykk og resulterende krefter på en bæreflate kan studeres med simuleringsprogrammet Foilsim som er utviklet av NASA Lewis Research Center. Bæreflatens form og areal kan endres. I tillegg kan programmet simulere en baseball med eller uten skru (spin). Programmet inneholder også noe grunnleggende lærestoff om aerodynamikk (Lesson) som hentes opp i et eget vindu mens simulatoren kjører.
Programmet må lastes ned til egen PC og installeres der.
Bildet nedenfor viser et skjermbilde fra programmet :

The program will run under Windows 3.x, 95, 98 or Windows NT. Click here to download a copy
of FoilSim {foilsim.zip} {1.09 Mb} in zip format.
To install,
If you don't have PKUNZIP, you can download this self-extracting file of FoilSim {foilsimzp.exe} {1.10 Mb}
Programmet er utviklet av
NASA Lewis Research Center.